Question

Using the example above as a guide, fill in the missing information. Enter percentage answers to the nearest tenth.

Jim Tree wants to analyze another shipment of Christmas trees based on height. He knows the height of the trees is normally distributed so he can use the standard normal distribution. He measures the height of 500 randomly selected trees in his shipment. Next, he calculates the mean and standard deviation of their heights. The mean is 60 inches and the standard deviation is 12 inches. Now, Jim uses the normal distribution table above to calculate the number of trees in each segment of the distribution.

Answer 1

Solution: We know that height of trees follows a normal distribution with mean height
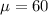`\mu=60` inches and standard deviation
`\sigma =12` inches

Now let's fill the missing values as per the normal distribution and the given information.

`a0=34.1\% of 500 = 0.341 * 500`

`=170.5 \approx 171`

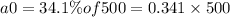
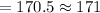
Now, let's find the value of a1. Since the height follows normal distribution with mean 60 and standard deviation = 12. Therefore, we have:

`a1=\mu+\sigma = 60+12=72`

To find the value of a2, we need to use the empirical rule of normal distribution. According to empirical rule, the area between Mean and 1 standard deviation above mean is 34.1%. Therefore, the value of a2 is:

`a2=34.1\%`

a3 denotes the area between +1 and +2 (72 to 84 inches). According to empirical rule of normal distribution, the area between one standard deviation above mean and two standard deviation mean is 13.6%.

`\therefore a3=13.6\%`

And
`a4=13.6\% of 500=0.136 * 500=68`

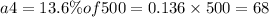
Therefore, the complete table is attached here.