slope intercept form is y=mx+b
So slope intercept form is The office manager of a small office ordered 140 packs of printer paper based on average daily use, she knows that the paper will last about 80 days
(A) Lets make a table
X axis represents the Number of days paper used
y axis represents the packs of printer paper used
x y
days packs of printer paper used
0 0 (0 days , 0 packs used)
80 140 (in 80 days , 140 packs paper used)
The graph is attached below
(B) To find Equation of a line we use points (0,0) and (80,140)
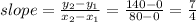
y intecept is (0,0)
so b= 4
Slope intercept form of a line i y=mx + b
m is the slope and b is the y intercept
So slope intercept form of line becomes
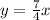
Standard form is Ax + By =C
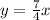
Multiply both sides by 4
4y = 7x
Now subtract 7x on both sides
-7x + 4y =0 is the standard form
(c) To find packs of printer paper the manager expect to have after 30 days, Plug in 30 for x and find out y
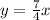
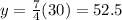
Total 140 packs of printer paper
52.5 packs of paper used
Packs of paper remaining after 30 days = 140- 52.5= 87.5