Question

Richard spent over $220 at an office supply store. He bought x reams of paper for $9 each and eight boxes of pens for $5 each. Model Richard's situation with an inequality, and solve for x. What can be interpreted about the solution of the inequality?

Answer 1

Richard's situation is expressed by the inequality 9x + 40 > 220, which solves to x > 20, meaning he bought more than 20 reams of paper. The minimum number of reams he could have purchased, therefore, is 21.

Step-by-step explanation:

To model Richard's situation with an inequality, we need to account for the cost of the reams of paper, which he bought at $9 each, and the cost of boxes of pens, which are $5 each for eight boxes. We are told that he spent over $220. So, the inequality representing this situation is:

9x + (8 × 5) > 220

Solving for x, we get:

1. Multiply the cost of each box of pens by the number of boxes: 8 × 5 = $40.
2. Subtract the total cost of the pens from the total amount spent: 220 - 40 = $180.
3. Divide the remaining amount by the cost of each ream of paper: 180 ÷ 9 = 20.

This means that Richard must have bought more than 20 reams of paper because x > 20.

From this solution, we can interpret that the minimum number of reams of paper Richard could have purchased is 21 reams, as he must have spent more than $220.

Answer 2

We are given

Richard spent over $220 at an office supply store

so, total money spent over =$220

He bought x reams of paper for $9 each

So, money spent on paper is

`=9x`

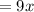
eight boxes of pens for $5 each

so, money spent on pens is

`=5* 8`

`=40`

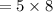
now, we can find total money spent

so, total money spent is

`=9x+40`

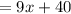
now, we are given maximum money he can spent over $220

we get

`9x+40\geq 220`

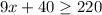
So, inequality is

`9x+40\geq 220`

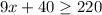
now, we can solve for x

Subtract both sides by 40

`9x+40-40\geq 220-40`

`9x\geq 180`

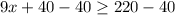
Divide both sides by 9

`x\geq 20`

Interpretation:

Since, x is the number of reams of paper

so, he can buy more than 20 reams of paper...........Answer