Answer
Therefore, the total length (in units) of the biking trail = 17 units
Step by step explanation
Here we have to use the distance formula to find the distance from P to Q, Q to R and R to S.
That is PQ, QR and RS
The distance formula =

PQ =
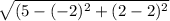
PQ =
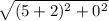
PQ = √7^2
PQ = 7
Now distance QR
Q = (5, 2) and R = (5, -5)
QR =
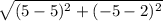
QR =

QR = √49
QR = 7
Now find the distance R and S
R = (5, -5) and S = (8, -5)
RS =

RS =
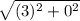
RS = √9
RS = 3
Therefore, the total length (in units) of the biking trail = PQ + QR + RS
= 7 + 7 + 3
= 17 units
Thank you. :)