Question

Select the correct answer from each drop-down menu.

Consider the first four terms of an arithmetic sequence below.

Answer 1

See Image... sorry.

Explanation:

Considering I guessed, this is pretty good!

Answer 2

The recursive function that describes this sequence is f(1) = 7, f(n) = f(n - 1) + 6, n ≥ 2.

The explicit function that describes this situation is f(n) = 6n + 1, and f(10) = 61.

In Mathematics and Geometry, the nth term of an arithmetic sequence can be calculated by using this equation:

`a_n=a_1+(n-1)d`

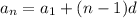
Where:

• d represents the common difference.
• 
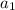  `a_1` represents the first term of an arithmetic sequence.
• n represents the total number of terms.

Next, we would determine the common difference for this arithmetic sequence as follows;

Common difference, d = succeding term - preceeding term

Common difference, d = 13 - 7 = 19 - 13 = 25 - 19

Common difference, d = 6.

Since the first term is 7, the recursive function can be writen as follows;

f(1) = 7, f(n) = f(n - 1) + 6, n ≥ 2.

For the explicit function, we have the following;

f(n) = 7 + (n - 1)6

f(n) = 7 + 6n - 6

f(n) = 6n + 1

Now, we can determine the 10th term;

f(10) = 6(10) + 1

f(10) = 61.