Question

Factor f(x)=x4-x3-7x2+13x-6 completely. Then Sketch the graph

Answer 1

ANSWER TO QUESTION 1

`f(x)=(x-2)(x+3)(x-1)^2`.

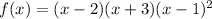Step-by-step explanation

The function given to us is,

`f(x)=x^4-x^3-7x^2+13x-6`

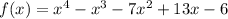
According to rational roots theorem,

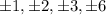`\pm1,\pm2,\pm3,\pm6` are possible rational zeros of

`f(x)=x^4-x^3-7x^2+13x-6`.

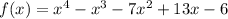We find out that,

`f(-3)=(-3)^4-(-3)^3-7(-3)^2+13(-3)-6`

`f(-3)=81+27-63-39-6`

`f(-3)=6-6`

`f(-3)=0`

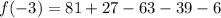
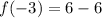
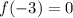
Also

`f(2)=(2)^4-(2)^3-7(2)^2+13(2)-6`

`f(2)=16-8-28+26-6`

`f(2)=6-6`

`f(2)=0`

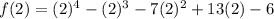
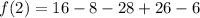
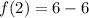
This implies that

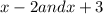`x-2 and x+3` are factors of

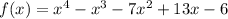`f(x)=x^4-x^3-7x^2+13x-6` and hence
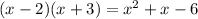`(x-2)(x+3)=x^2+x-6` is also a factor.

We perform the long division as shown in the diagram.

Hence,

`f(x)=(x-2)(x+3)(x-1)^2`.

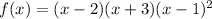ANSWER TO QUESTION 2

Sketching the graph

We can see from the factorization that the roots

`x=2` and
`x=-3` have a multiplicity of 1, which is odd. This means that the graph crosses the x-axis at this intercepts.

Also the root
`x=1` has a multiplicity of 2, which is even. This means the graph does not cross the x-axis at this intercept.

Now we determine the position of the graph on the following intervals,

`x\le -3`

`f(-4)=(-4)^4-(-4)^3-7(-4)^2+13(-4)-6`

`f(-4)=150\:>0`

`-3\le x \le 1`

`f(0)=-6\:<0`

`1\le x\le 2`

`f(1.5)=-0.56\:<0`

`x \ge 2`

`f(3)=24\:>0`

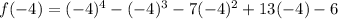
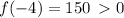
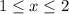
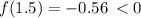
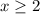
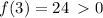
We can now use these information to sketch the function as shown in diagram