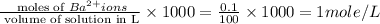Answer : The molarity of each type of ion remaining in solution are :
Molarity of
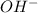 ions = 0.8 mole/L
ions = 0.8 mole/L
Molarity of
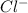 ions = 1.2 mole/L
ions = 1.2 mole/L
Molarity of
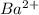 ions = 1 mole/L
ions = 1 mole/L
Explanation:
The given reaction is,
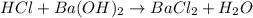
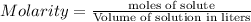

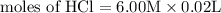 = 0.12
= 0.12
As 1 mole of HCl dissociates to give 1 mole of
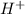 and 1 mole of
and 1 mole of
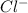
So, 0.12 mole of HCl dissociates to give 0.12 mole of
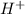 and 0.12
and 0.12
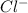
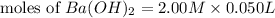 = 0.1
= 0.1
As 1 mole of
 dissociates to give 2 moles of
dissociates to give 2 moles of
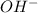 ions,
ions,
So, 0.1 moles of
 dissociates to give 0.1 moles of
dissociates to give 0.1 moles of
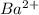 and 0.2 moles of
and 0.2 moles of
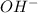
As 0.12 mole of
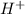 ions will neutralize 0.12 moles of
ions will neutralize 0.12 moles of
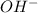 ions.
ions.
So, remaining
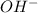 ions in the solution will be 0.2 - 0.12 = 0.08 moles
ions in the solution will be 0.2 - 0.12 = 0.08 moles
So, moles of
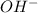 ions after the reaction = 0.08 moles
ions after the reaction = 0.08 moles
Now we have to calculate the molarity of each type of ions remaining in solution.
Total volume = 20 + 30 + 50 = 100 ml
Molarity of
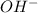 ions =
ions =
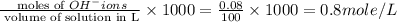
Molarity of
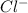 ions =
ions =
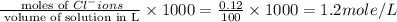
Molarity of
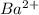 ions =
ions =