Question

Graph the following piecewise function
please wait wile i upload my image

Answer 1

see attached

Explanation:

Piecewise functions have multiple pieces of curves/lines where each piece corresponds to its definition over an interval.

Given piecewise function:

`\begin{aligned}f(x)=\begin{cases}2 & \textsf{if} \quad 2 < x\leq 4\\x+3 & \textsf{if} \quad 4 < x < 8\\2x & \textsf{if} \quad x\geq 8\end{cases}\end{aligned}`

Therefore, the function has three definitions:

• 
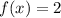  `f(x)=2` when x is more than 2 or less than or equal to 4.
• 
  `f(x)=x + 3` when x is more than 4 or less than 8.
• 
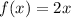  `f(x)=2x` when x is more than or equal to 8.

Use open circle where the value of x is not included in the interval.

Use closed circle where the value of x is included in the interval.

Use an arrow to show that the function continues indefinitely.

First piece of function

Substitute the endpoints of the interval into the corresponding function:

• f(2) = 2
• f(4) = 2

Place an open circle at point (2, 2) and a closed circle at (4, 2).

Join the points with a straight line.

Second piece of function

Substitute the endpoints of the interval into the corresponding function:

• f(4) = 4 + 3 = 7
• f(8) = 8 + 3 = 11

Place an open circle at point (4, 7) and an open circle at (8, 11).

Join the points with a straight line.

Third piece of function

Substitute the endpoint of the interval into the corresponding function:

• f(8) = 2(8) = 16
• f(10) = 2(10) = 20

Place a closed circle at (8, 16).

Plot another point where x > 8 (for purposes of helping draw the line).

Draw a straight line beginning at (8, 16) and continuing through (10, 20) with an arrow at the end.