Question

What causes a solution to a rational equation to be an extraneous solution?

Answer 1

If a solution results in zero when substituted into the denominator of the equation, the solution is extraneous.

Answer 2

Extraneous solution:

An extraneous solution is a solution that arises from the solving process that is not really a solution at all

So, firstly we will solve for the equation

and then we verify each solutions by plugging them back

If denominator of rational equation becomes zero , then that solution must be extraneuous solution

For example:

`(1)/(x+3) +(2)/(x) =-(3)/(x(x+3))`

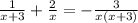
we can solve for x

Multiply both sides by x(x+3)

`(1)/(x+3)x\left(x+3\right)+(2)/(x)x\left(x+3\right)=-(3)/(x\left(x+3\right))x\left(x+3\right)`

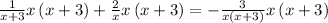
now, we can simplify it

`x+2\left(x+3\right)=-3`

`x+2x+6=-3`

`3x=-9`

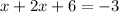
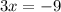
now, we can solve for x

`x=-3`

now, we can check whether x=-3 is extraneous solution

we will plug back x=-3 into original

`(1)/(-3+3) +(2)/(-3) =-(3)/(-3(-3+3))`

`(1)/(0) +(2)/(-3) =-(3)/(-3(0))`

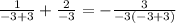
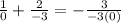
we can see that denominator becomes 0

so, x=-3 can not be solution

so, x=-3 is extraneous solution...........Answer