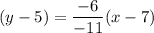Answer:
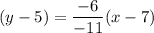
Explanation:
We know that the point slope form of a line that passes through two points (a,b) and (c,d) is given by :-

Similar;y , the equation in point-slope form of the line that passes through the points (7, 5) and (−4, −1) will be :-
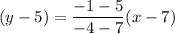
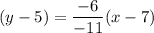
Hence, the equation in point-slope form of the line that passes through the points (7, 5) and (−4, −1) is given by :-