Question

the average snow fall in lake Hopatcong is normally distributed. The average snowfall equals 56 inches. the average snow fall in lake Hopatcong exceeds 59 inches in 15% of the year. what is the standard deviation?

Answer 1

Solution: We are given that average snowfall in lake Hopatcong is normally distributed with mean
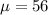`\mu =56` inches

The average snowfall in lake Hopatcong exceeds 59 inches in 15% of the year.

Therefore, the z score corresponding to less 59 inches is
`z(0.85)=1.0364`

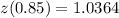
Using the z-score formula, we have:

`z=(x-\mu)/(\sigma)`

`1.0364=(59-56)/(\sigma)`

`\sigma = (59-56)/(1.0364)`

`\sigma = (3)/(1.0364)`

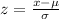
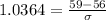
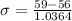
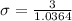
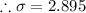`\therefore \sigma =2.895` rounded to 3 decimal places

Hence the standard deviation is 2.895 inches