Answer : The an explicit formula for the arithmetic sequence will be,

Step-by-step explanation :
Arithmetic progression : It is a sequence of numbers in which the difference of any two successive number is a constant.
The general formula of arithmetic progression is:
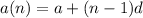
where,
a(n) = nth term in the sequence
a = first term in the sequence
d = common difference
n = number of terms in the sequence
As we are given that:
Common difference = d = -18
Thus, the formula of arithmetic progression will be:
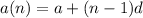
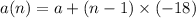

For example:
Let n=1 :
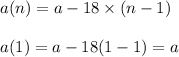
Let n=2 :
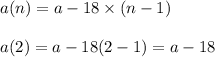
Let n=3 :
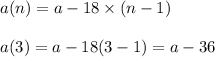
The sequence will be, a, (a-18), (a-36),.........
Thus, the an explicit formula for the arithmetic sequence will be,
