Question

In the equation square root n+5-square root n-10=1 the value of n is

Answer 1

the value of n is 59

Explanation:

plato says it was right (:

Answer 2

square root n+5-square root n-10=1

`√(n+5) - √(n-10) =1`

add sqrt(n-10) on both sides

`√(n+5) =1+ √(n-10)`

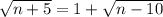
To remove square root we take square on both sides

`(√(n+5))^2 =(1+ √(n-10))^2`

`n+5=(1+ 2√(n-10) +n -10)`

`n+5=2√(n-10) +n -9`

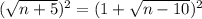
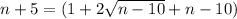
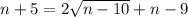
Subtract n and add 9 on both sides

`14=2√(n-10)`

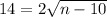
Now we divide both sides by 2

`7=√(n-10)`

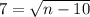
Take square on both sides

+-49= n - 10

49 = n-10 and -49 = n - 10

Add 10 on both sides

n= 59 and n = -39

Now we verify both solutions

When n = -39 we will get negative under the square root . that is complex so we ignore n=-39

n = 59 is our solution