Question

PLEASE

CD is perpendicular to AB and passes through point C(5, 12). If the coordinates of A and B are (-10, -3) and (7, 14), respectively, the x-intercept of CD is ____ . The point ____ lies on CD .


blank one
1)12,0
2)15,0
3)17,0
4)19,0


blank two

1)-5,24
2)-2,19
3)7,-10
4)8,11

Answer 1

First find the gradient of line AB

14--3/7--10

17/17 = 1

As CD is perpendicular to AB take the negative reciprocal of the gradient to AB to find gradient of CD

Gradient of CD = -1

to find y intercept use points given

12=(-1 x 5) +c

17 = c

C is the y intercept so for question 1 the answer is 3

for the second question just plug values into the equation and see if you get the right y value

Here the only number that works is -2

for question 2

the answer is 2

Answer 2

First blank (17,0)

Option 3 is correct

Second Blank (-2,19)

Option 2 is correct

Explanation:

CD is perpendicular to AB

C(5,12)

A(-10,-3)

B(7,14)

CD ⊥ AB

Thus, Slope of CD is negative inverse of slope of AB

`\text{Slope of AB }=(14+3)/(7+10)`

`m=1`

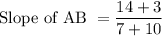
Slope of CD, m=-1 (CD ⊥ AB )

Point C: (5,12)

Equation of line CD,

`y-12=-1(x-5)`

`y=-x+17`

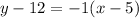
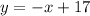
For x-intercept: Put y=0

`0=-x+17`

`x=17`

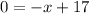
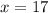
x-intercept: (17,0)

For second blank we have to check each point.

Option 1: (-5,24) ,Put x=-5 and y=24

`24=5+17`

`24\\eq 22`

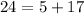
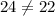
False

Option 2: (-2,19) ,Put x=-2 and y=19

`19=2+17`

`19=19`

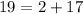
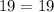
True

Option 3: (7,-10) ,Put x=7 and y=-10

`-10=-7+17`

`-10\\eq 10`

False

Option 4: (8,11) ,Put x=8 and y=11

`11=-8+17`

`11\\eq 9`

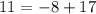
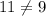
False

Hence, First blank (17,0) and Second blank (-2,19)