Question

In a parallelogram EFGH, EJ=x^2-4 and JG=3x. What is EG?

Answer 1

Answer : The value of side EG is, 24 units.

Step-by-step explanation :

Property of parallelogram:

The diagonals bisect each other and the opposite sides are equal to each other.

In the given parallelogram EFGH,

Given:

Side EJ =
`x^2-4`

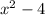
Side JG = 3x

According to the property of parallelogram,

Side EJ = Side JG

`x^2-4=3x`

`x^2-3x-4=0`

`x^2-4x+1x-4=0`

`x(x-4)+1(x-4)=0`

`(x-4)(x+1)=0`

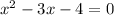
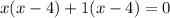
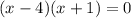
(x-4) = 0 and (x+1) = 0

x = 4 and x = -1

Now we have to determine the value of side EG.

Side EG = Side EJ + Side JG

Side EG =
`x^2-4+3x`

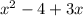
Now put the value of x = 4, we get:

Side EG =
`(4)^2-4+3(4)=16-4+12=24`

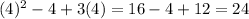
Now put the value of x = -1, we get:

Side EG =
`(-1)^2-4+3(-1)=1-4-3=-6`

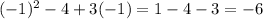
As we know that, the value of side can not be negative. So, the value of side EG will be, 24 units.

Hence, the value of side EG is, 24 units.

Answer 2

EG = 24 ( solution is attached below)