Question

Please help!!!
Composition of functions~

Answer 1

`\left(g\:\circ \:\:\:h\right)\left(-4\right)=-2`

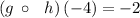
Hence, option B) is true.

Explanation:

Given

g(t) = t² - 2

h(t) = t + 4

To determine

`\left(g\:\circ \:\:h\right)\left(-4\right)=?`

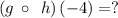
Using the formula

`\left(g\:\circ \:\:h\right)\left(-4\right)\:=g\left(h\left(-4\right)\right)`

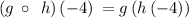
In order to determine g(h(-4)), first we need to determine h(-4), so

substituting t = -4 in h(t) = t + 4

h(t) = t + 4

h(-4) = -4 + 4

h(-4) = 0

so we can write

`\left(g\:\circ \:\:\:h\right)\left(-4\right)\:=g\left(h\left(-4\right)\right)=g\left(0\right)`

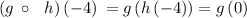
now, to determine g(0), substitute t = 0 in g(t) = t² - 2v

g(t) = t² - 2

g(0) = (0)² - 2

g(0) = 0 - 2

g(0) = -2

so, finally we get

`\left(g\:\circ \:\:\:h\right)\left(-4\right)\:=g\left(h\left(-4\right)\right)=g\left(0\right)=-2`

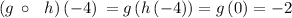
Therefore,

`\left(g\:\circ \:\:\:h\right)\left(-4\right)=-2`

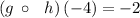
Hence, option B) is true.