Question

Which equation is not a function?
2+x-x2=14
x2-x-10=24
y2+3x=6
2y+3x=6

Answer 1

The correct options are 1,2 and 3.

Step by step explanation:

According to the definition of function there exist unique value of y for each value of x in the domain of the function.

If equation have more than one values of y for any value of x, then the equation is not a function.

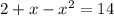`2+x-x^2=14` .... (1)

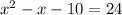`x^2-x-10=24` ... (2)

A quadratic equation have two values of x and the value of y can be any number. So a quadratic equation is not a function.

The first and second equations are quadratic equations so the equation (1) and (2) are not functions.

The third equation is

`y^2+3x=6`

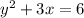
The degree of y is 2. It means for each value of x there exist two values of y.

Put x=0, then we get

`y=\pm √(6)`

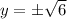
More than one values of y exist for single value of x.

So the equation (3) is not a function.

The fourth equation is

`2y+3x=6`

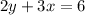
Since the degree of x is 1 and degree of y is also 1, therefore it is a linear equation and for each value of x there exist a unique value of y.

Therefore the equation (4) is a function.