Question

100 points....

The graph below is a solution to what system of linear inequalities?

Answer 1

Answer: The answers are given below.

Step-by-step explanation:

(i) For the first figure:

We can clearly see from the graph that A(0,1) and B(1,2) are two points on the dark line. So, slope of the dark line is

`m=(2-1)/(1-0)=1.`

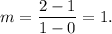
Therefore, the equation of the line will be

`y-1=1(x-0)\\\\\Rightarrow x-y=-1.`

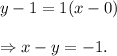
Also, C(0,-2) and D(-2,0) are points on the dotted line. solving similarly as above, we find the equation of the dotted line as

`x+y=-2.`

Since the first line is dark and second is dotted and looking at the common shaded region, we find the pair of inequalities as follows

`x-y\leq-1,\\\\x+y>-2.`

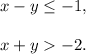
(ii) For the second figure, the given inequalities are

`y<x+2,\\\\y\leq-(3)/(4)x.`

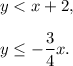
Plotting these two inequalities on a graph paper, we can see the dotted line represents the boundary for the first inequality and dark line represents the boundary for the second inequality. The shaded portion represents the solution. Please see the attached figure.

Answer 2

The system of linear inequalities is

`y\geq x+1`

`y>-x-2`

Explanation:

From the given graph it is noticed that we have two lines one is solid and second is dashed.

The solid line passing through the points (0,1) and (-1,0). The dashed line passing through the points (0,-2) and (-2,0).

If line passing through two points, then the equation of line is

`y-y_1=(y_2-y_1)/(x_2-x_1)(x-x_1)`

The related equation of solid line is

`y-1=(0-1)/(-1-0)(x-0)`

`y=x+1`

Similarly the related equation of dashed line is

`y-(-2)=(0-(-2))/(-2-0)(x-0)`

`y=-x-2`

From the given figure it is noticed that the point (0,2) is in the shaded region, it means the point (0,2) will satisfy the inequalities.

`2=0+1`

`2=1`

This statement will true if the sign of inequality is
`\geq` because It is a solid line.

`2=-0-2`

`2=-2`

This statement will true if the sign of inequality is > because It is a dashed line.

The system of linear inequalities is

`y\geq x+1`

`y>-x-2`