Question

Find the value of c so that (x-5) is a factor of the polynomial p(x)

Answer 1

I think the question is

Find the value of c so that (x-5) is a factor of the polynomial

`p(x) = x^3 + 2x^2 + cx + 10`

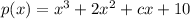
The other factor is going to be some quadratic. We can say a few things about its coefficients but let's start by saying in general it's

`q(x)= ax^2 + bx + k`

`p(x) = (x-5)q(x)`

`x^3 + 2x^2 + cx + 10 = (x-5)(ax^2 + bx+k) = ax^3 + (b-5a)x^2 + (k-5b)x - 5k`

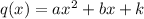
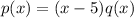
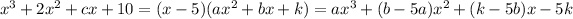
Equating respective coefficients,

`a=1`

`b-5a = 2`

`k - 5b = c`

`-5k = 10`

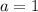
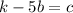
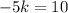
so we get

`b = 2 + 5 = 7`

`k = 10/-5 = -2`

`c = k - 5b = 2 - 5(7)= -37`

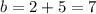
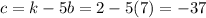
Answer: -37

Check:

`(x^2 + 7x - 2)(x - 5) = x^3 + 2 x^2 - 37 x + 10\quad\checkmark`