Question

N is a multiple of 5

A = N + 1
B = N – 1
Prove, using algebra, that A2 – B2 is always a multiple of 20

Answer 1

Proved

`A^2 - B^2 = 20, 40,60,80...`

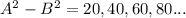
Explanation:

Given

`A = N + 1`

`B = N - 1`

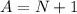
Required

Prove that
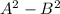`A\² - B\²` is a multiple of 20

First, we need to evaluate
`A\² - B\²`

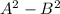
Start by applying difference of two squares

`A\² - B\² = (A + B)(A - B)`

Substitute values for A and B

`A\² - B\²= (N + 1 + N - 1)(N + 1 -(N-1))`

`A\² - B\² = (N + 1 + N - 1)(N + 1 - N + 1)`

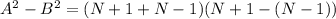
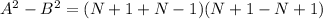
Collect Like Terms

`A\² - B\² = (N + N+ 1 - 1)(N - N + 1+ 1)`

`A\² - B\² = (2N)(2)`

`A\² - B\² = 2N*2`

`A\² - B\² = 4N`

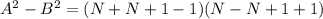
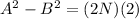
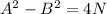
Since, N is a multiple of 5, then the possible values of N are:

`N = 5, 10, 15, 20...`

For each of these values, the possible values of
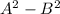`A^2 - B^2` are

`A^2 - B^2 = 4N: 4 * 5, 4*10,4*15,4*20...`

`A^2 - B^2 = 20, 40,60,80...`

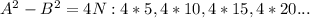
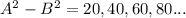
The above shows that
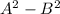`A^2 - B^2` is a multiple of 20