Answer:
The correct option is C.
Explanation:
The given equation is
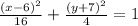
It can be rewritten as
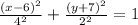 .....(1)
.....(1)
The standard form of an ellipse is
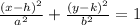 ....(2)
....(2)
Where (h,k) is center of the ellipse.
If a>b, then the vertices of the ellipse are
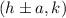 .
.
From (1) and (2) we get
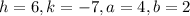
Since a>b, therefore the vertices of the ellipse are
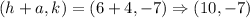
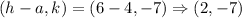
The vertices of the given ellipse are (10, –7) and (2, –7). Therefore the correct option is C.