Answer:
Length of BD = 108 units
Explanation:
Given: In parallelogram ABCD , BE = 7x-2 and DE =
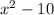 .
.
Segment AC intersects segment BD at point E.
Properties of parallelograms:-
- Opposite sides are congruent (AB=CD)
- Opposite angels are congruent (D=B).
- Also, consecutive angles are supplementary (A + D = 180°).
- Diagonals of a parallelogram bisect each other.
- Every diagonal of a parallelogram separates it into two congruent.
The diagonal BD;
BD = BE + ED
since, by properties of parallelogram;
BE = ED ......[1]
Substitute the given values of BE and DE in [1] to solve for x;
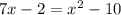
or
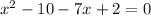

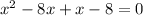
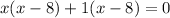
(x-8)(x+1) = 0
equate each factor equals to 0 we get;
x = 8 and x = -1
Since sides are always in positive,
⇒x =8
Then;
BE = 7x -2 = 7(8) -2 = 56-2 = 54 units.
To find the Length of BD:
As we know;
BD = BE + ED = BE + BE = 2BE [Since, BE = ED]
BD =
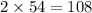 units
units
Therefore, the length of BD is 108 units.