Question

What is the equation of this graphed line? Enter your answer in slope-intercept form in the box.

Answer 1

`y=-(9)/(8)x+7`

Step-by-step explanation:

we know that

The equation of the line into slope intercept form is equal to

`y=mx+b`

where

m is the slope

b is the y-coordinate of the y-intercept

In this problem we have

`b=7` ------> because the point
`(0,7)` is the y-intercept

point
`(8,-2)`

substitute the value of x , y and b in the equation to solve for m

`y=mx+b`------>
`-2=m(8)+7`

`m(8)=-2-7`

`m=-9/8`

therefore

the equation is equal to

`y=-(9)/(8)x+7`

Answer 2

Answer: The slope intercept form of the line is
`y=-(9)/(8)x+7`.

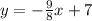Step-by-step explanation:

From the figure it is noticed that the line passing through two points (0,7) and (8,-2).

If a line passing through two points then the equation of line is,

`y-y_1=(y_2-y_1)/(x_2-x_1) (x-x_1)`

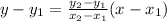
The lines passing through (0,7) and (8,-2),

`y-7=(-2-7)/(8-0) (x-0)`

`y-7=(-9)/(8) (x)`

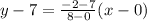
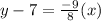
Add 7 to both sides.

`y=(-9)/(8) (x)+7`

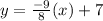
Therefore, the slope intercept form of the line is
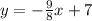`y=-(9)/(8)x+7`.