Given problem is
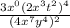
distribute outer exponents using formula:
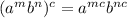 , we get:
, we get:
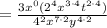
Simplify exponents:
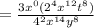
plug
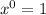
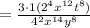
simplify exponents
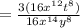
simplify (closure property)
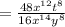
simplify exponent part using formula :
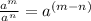 we get:
we get:
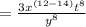
Simplify exponents:
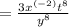
send term to denominator to avoid negative exponent
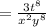
Hence final answer is
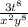 .
.