Answer:
Using properties of parallelogram and angle sum property of a triangle in the figure as shown below in the attachment
In parallelogram ABCD, AC is a diagonal.
Given:
 and
and
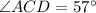
As, we know that opposite angles in parallelogram are equal.
therefore,
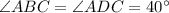
Now, in ΔADC
Sum of the measures of angles in a triangle is 180 degree.
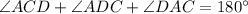
Substituting the values of
 and
and
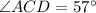 we have;
we have;
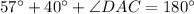
or
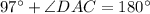
Subtract
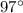 from both sides we get
from both sides we get
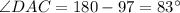
Therefore, the measure of angle CAD is
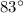 .
.