Question

What is the slope of the line that is perpendicular to the line shown on the graph?

Answer 1

since the slope of this line is -1/4, the slope of the perpendicular line would be 4.

Answer 2

the slope of the line that is perpendicular to the line shown is 4

Explanation:

Hello

Step 1

find the slope of the line shown using

`m=(y_(2)-y_(1))/(x_(2)-x_(1)) \\where\\(x_(1),y_(1)) and (x_(2),y_(2)) are\ the\ coordinates\ of\ two\ known\ points\\`

Let

P1(0,2)

P2(4,1)

replacing

`m=(y_(2)-y_(1))/(x_(2)-x_(1))\\m=(1-2)/(4-0)\\m=(-1)/(4)\\ m=-(1)/(4)`

`m_(1)=-(1)/(4)`

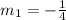
Step 2

two lines are perpendicular when

`m_(1) *m_(2)=-1\\ m_(1) =-(1)/(4) \\solve\ for\ m_(2)\\m_(1) * m_(2)=-1\\m_(2)=-(1)/(m_(1) )\\replace\\m_(2)=-(1)/(-(1)/(4) ) \\m_(2)=(4)/(1) \\m_(2)=4`

the slope of the line that is perpendicular to the line shown is 4

Have a good day