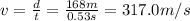Question

Madelin fires a bullet horizontally. The rifle is 1.4 meters above the ground The bullet travels 168 meters horizontally before it hits the ground. What speed did Madelin's bullet have when it exited the rifle?

Answer 1

Considering the parabolic moment, the time upto which the bullet was in air will be given by below equation:

Y = Y0 + V0y x t - 1/2 gt^2

Y0 = initial height

Y= Final height

0 = 1.4 + 0 - 0.5 x 9.8 m/s^2 x t^2

t= 0.533 seconds

Speed of bullet = distance traveled /time taken

= 168 m/0.533 seconds

= 315 m/s

Answer 2

Answer: 317.0 m/s

Step-by-step explanation:

The motion of the bullet is a projectile motion, with:

- a uniform motion with constant speed v along the horizontal direction

- an accelerated motion with constant acceleration
`g=-9.81 m/s^2` toward the ground

We know that the starting height of the bullet is h=1.4 m. If we consider the vertical motion only, the initial velocity is zero, so we can write:

`y(t)=h+(1)/(2)gt^2`

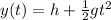
The bullet reach the ground when y(t)=0, so the time taken is

`0=h+(1)/(2)gt^2\\t=\sqrt{-(2h)/(g)}=\sqrt{(-2(1.4 m))/(-9.81 m/s^2)}=0.53 s`

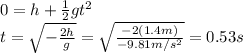
During this time, the bullet travels d=168 m horizontally, so its horizontal speed (which is equal to the initial speed of the bullet) is given by

`v=(d)/(t)=(168 m)/(0.53 s)=317.0 m/s`