Question

In △ABC, point M is the midpoint of AB , point D∈ AC so that AD:DC=2:5. If AABC=56 yd2, find ABMC, AAMD, and ACMD.

Answer 1

Answer: The area of BMC is 28 yd square, the area of AMD is 8 yd square and the area of CMD is 20 yd square.

Step-by-step explanation:

It is given that the M is the midpoint of the side AB. The line MC is the median of the triangle ABC.

A median divides the area of triangle in two equal parts, therefore the area of triangle BMC is half of the area of triangle ABC.

`\text{ Area of }\triangle BMC =(1)/(2)* \text{ Area of }\triangle ABC}`

`\text{ Area of }\triangle BMC =(1)/(2)* 56}`

`\text{ Area of }\triangle BMC =28`

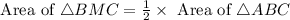
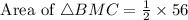
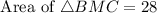
Therefore the area of BMC and AMC is 28 yd square.

Draw a perpendicular on AD from M as shown in the figure.

`\frac{\text{ Area of }\triangle AMD}{\text{ Area of }\triangle AMC}= ((1)/(2)* AD* ME)/((1)/(2)* AC* ME) =(AD)/(AC)= (2)/(7)`

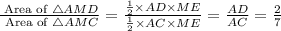
Therefore the area of AMD is
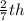`(2)/(7)th` part of the area of AMC.

`\text{ Area of }\triangle AMD =(2)/(7)* \text{ Area of }\triangle AMC}`

`\text{ Area of }\triangle AMD =(2)/(7)* 28`

`\text{ Area of }\triangle AMD =8`

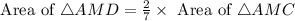
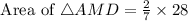
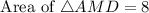
Therefore the area of AMD is 8 yd square.

`\text{ Area of }\triangle CMD=\text{ Area of }\triangle ABC-\text{ Area of }\triangle AMD-\text{ Area of }\triangle BMC`

`\text{ Area of }\triangle CMD=56-8-28=20`

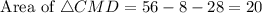
Therefore the area of CMD is 20 yd square.