Question

Could someone answer and explain these please? Thank you!

Answer 1

Answer 1:

It is given that the positive 2 digit number is 'x' with tens digit 't' and units digit 'u'.

So the two digit number x is expressed as,

`x=(10 * t)+(1 * u)`

`x=10t+u`

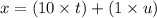
The two digit number 'y' is obtained by reversing the digits of x.

So,
`y=(10 * u)+(1 * t)`

`y=10u+t`

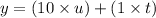
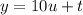
Now, the value of x-y is expressed as:

`x-y=(10t+u)-(10u+t)`

`x-y=10t+u-10u-t`

`x-y=9t-9u`

`x-y=9(t-u)`

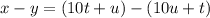
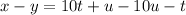
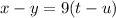
So,
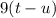`9(t-u)` is equivalent to (x-y).

Answer 2:

It is given that the sum of infinite geometric series with first term 'a' and common ratio r<1 =
`(a)/(1-r)`

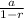
Since, the sum of the given infinite geometric series = 200

Therefore,
`(a)/(1-r)=200`

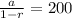
Since, r=0.15 (given)

`(a)/(1-0.15)=200`

`(a)/(0.85)=200`

`a=0.85 * 200`

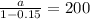
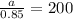
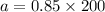
a=170

The nth term of geometric series is given by
`ar^(n-1)`.

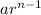So, second term of the series =
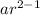`ar^(2-1)` = ar

Second term =
`170 * 0.15`

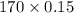
= 25.5

So, the second term of the geometric series is 25.5

Explanation: