Question

The product of two consecutive even number is 168. find the numbers

Answer 1

even numbers can be represented as 2n where n is an integer

consecutive even integers are 2 apart (2,4,6,8, etc)

so 2 consecutive even integers can be represeted as 2n and 2n+1

their product is 168, so

(2n)(2n+2)=168

expand/distribute

4n²+4n=168

factor out a 4

4(n²+n)=168

divide both sides by 4

n²+n=42

solve by completing the square

take 1/2 of the linear coefient and square it

the linear coeffient is 1 so 1/2 of 1 is 1/2, and (1/2)^2=1/4

add 1/4 to both sides

n²+n+1/4=42+1/4

factor perfect square trinomial

`(n+(1)/(2))^2=42.25`

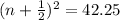
square root both sides

`n+(1)/(2)=\pm 6.5`

subract 1/2 from both sides

`n=-0.5 \pm 6.5`

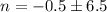
n=-0.5+6.5 or -0.5-6.5

n=6 or -7

if n=6, then 2n=12 and 2n+2=12+2=14

if n=-7, then 2n=-14 and 2n+2=-14+2=-12

so the 2 numbers are 12 and 14 or -12 and -14 (the problem didn't specify the sign of the numbers)

Answer 2

Hello from MrBillDoesMath!

Answer: 12

Steps:

Let "n" be the smaller even integer. Then next consecutive even integer is n+2. The questions us to find "n" given that n (n+2) = 168. We can solve this using the quadratic equation or using the approach shown below:

n(n+2) = 168

is equivalent to

n^2 + 2n = 168.

Add 1 to both side to get

n^2 + 2n + 1 = 168 + 1= 169 = 13^2.

But n^2 + 2n +1 = (n+1) ^2, so we have

(n+1)^2 = 13^2

giving

n+1 = 13

or n = 13-1 = 12

Let's check: 12 * (12 +2) = 12 ^ 14 =-168

Regards, MrB