Question

Which is easier?

Completing the square
or
Quadratic formula

Please explain

Answer 1

the quadratic formula is derived by completing the square

in other words, by using the quadratic formula, you do complete the square but you skip straight to the answer

below is the derivation of the quadratic formula just for fun

note: I used the method of completing the square to derive the formula

ax²+bx+c=0

group like terms

(ax²+bx)+c=0

factor out quadratic coefient

`a(x^2+(b)/(a)x)+c=0`

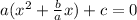
take 1/2 of linear coefient and square it

(b/a)/2=b/(2a), ((b/(2a))^2=(b^2)/(4a^2)

add positive and negative of it inside parntheasees

`a(x^2+(b)/(a)x+(b^2)/(4a^2)-(b^2)/(4a^2))+c=0`

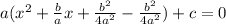
factor perfect square trinomial

`a((x+(b)/(2a))^2-(b^2)/(4a^2))+c=0`

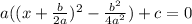
expand

`a(x+(b)/(2a))^2-(b^2)/(4a)+c=0`

add (b^2/4a-c) to both sides

`a(x+(b)/(2a))^2=(b^2)/(4a)-c`

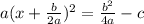
divide by both sides by a

`(x+(b)/(2a))^2=(b^2)/(4a^2)-(c)/(a)`

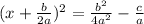
before we go on, combine right side into 1 fraction

(c/a)(4a/4a)=4ac/4a^2, so
`(b^2)/(4a^2)-(c)/(a)=(b^2-4ac)/(4a^2)`

`(x+(b)/(2a))^2=(b^2-4ac)/(4a^2)`

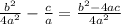
square root both sides

`x+(b)/(2a)=\pm \sqrt{(b^2-4ac)/(4a^2)}`

`x+(b)/(2a)=(\pm √(b^2-4ac))/(2a)`

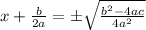
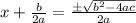
subtract
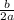`(b)/(2a)` from both sides

`x=(-b \pm √(b^2-4ac))/(2a)`

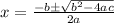
in conclusion, the quadratic formula completes the square for you and is therefore faster when you are given the function in standard form (0=ax²+bx+c).

Answer 2

It depends. Everyone have there own preferences . I myself use the completing square method because I can do it fast. But many of my colleagues use quadratic formula. so there is no such thing as which one is easier.

Solve x2−6x−3=0

x2−6x=3
x2−6x+(−3)2=3+9
(x−3)^2=12
take square root on both sides
x−3=±12
x= 3 ±2√3