Question

$5000 is invested at 6.75% continuously compounding. What is the time, in years, for the investment to double? Answer to the nearest hundredths place.

________ years

Answer 1

Use formula to calculate continuously compounded interest

`A=P\cdot e^(rt),`

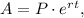
where

P is the principal (initial) balance,

r is the rate of interest,

t is the time in years.

In your case, P=$5000, r=0.0675, A=$10000 (the amount of money should be doubled), then

`\$10000=\$5000\cdot e^(0.0675t),\\ \\e^(0.0675t)=2,\\ \\0.0675t=\ln 2,\\ \\t=(\ln 2)/(0.0675)\approx 10.3.`

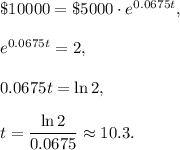
Therefore, you need about 10.3 years for the investment to double. If you consider the whole years, then you need 11 years.

Answer: 11 years