Answer: There are
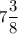 laps in all.
laps in all.
Explanation:
Since we have given that
Number of laps must run by first team =
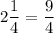
Number of laps must run by second team =
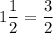
Number of laps must run by third team =
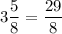
So, total number of laps in all must run is given by
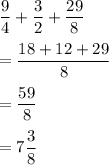
Hence, there are
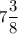 laps in all.
laps in all.