Question

PLZ HELP! Need this real bad! Thx so much!

Given: AB ≅ BC and AE = 10 in
m∠FEC = 90°
m∠ABC = 130°30'
Find: m∠EBC, AC

Plz show ur work! Thx again :)

Answer 1

`\boxed{\boxed{m\angle EBC=65^(\circ)15'}}\\\\\boxed{\boxed{AC=20\ in}}`

Solution-

The ΔABC is an isosceles triangle, as AB = BC

And m∠FEC=90°, so m∠BEC=90° (as they are complimentary angle)

Hence, BE is an altitude to the base.

From the properties of an isosceles triangle (where base is the side which is not equal to any other side), we know that

The altitude drawn to the base is the median and the angle bisector.

So,

`\Rightarrow m\angle ABC=2* m\angle EBC`

`\Rightarrow m\angle EBC=(1)/(2)m\angle ABC=(1)/(2)* 130^(\circ)30'`

`\Rightarrow m\angle EBC=65^(\circ)15'`

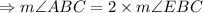
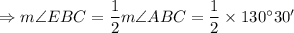
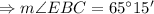
And also,

`AC=2* AE=2* 10=20\ in`