Question

1. Alicia has 7 paintings she wants to hang side by side on her wall.

A. In how many ways can she arrange all 7 paintings to create a different look from left to right each time? Show your work.

B. If she only wants to display 3 of the paintings, in how many different groups of 3 can she choose the paintings? Show your work.

C. If Alicia wants to have the 3 out of 7 paintings in specific places, how many ways could she order the 3 paintings? Show your work.

Answer 1

solution is attached below

Answer 2

A.

If we take 7 paintings to be hung in 7 spaces side by side, the first space can have any one of the 7 paintings, the second space can have any one of the remaining 6 paintings (as 1 is already hung), the third space can have any one of the remaining 5 paintings (as 2 already hung)...It goes on like this.

So we have
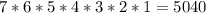`7*6*5*4*3*2*1=5040` ways to arrange all the paintings from left to write. (in factorial notation it is 7!=5040)

B.

We use combinations rather than permutations because order doesn't matter. If we name the paintings A,B,C,D,E,F, and G, groups of 3 paintings of ABC or ACB are the same. So we evaluate
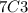`7C3` using the combination formula,

`nCr=(n!)/((n-r)!r!)`

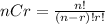
We have,

`7C3=(7!)/((7-3)!*3!) = (7!)/(4!*3!) = 35`

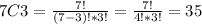
C.

This is similar to part A in some ways. Any 3 pictures can be arranged in
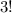`3!` different ways.
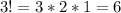`3!=3*2*1=6`. So, 6 different ways.

ANSWER:

A) 5040 ways

B) 35 different groups

C) 6 ways