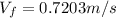Question

A solid block, with a mass of 8.58kg, on a frictionless surface is pushed directly onto a horizontal spring, with a spring constant value of 368N/m, until the spring is compressed by 11cm. The block is then released. What is the block's final speed, in m/s?

Answer 1

In this problem, we are talking about Mechanical Energy (
`M`) which is the addition of the Kinetic Energy
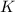`K` (energy of the body in motion) and Potential Energy
`P` (It can be Gravitational Potential Energy or Elastic Potential Energy, in this case is the second):

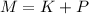`M=K+P` (1)

The Kinetic Energy is:
`K=(1)/(2)mV^(2)`

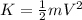
Where
`m` is the mass of the body and
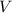`V` its velocity

And the Potential Energy (Elastic) is:
`P=(1)/(2)cX^(2)`

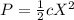
Where
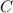`C` is the spring constant and
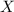`X` is the the position of the body.

Knowing this, the equation for the Mechanical Energy in this case is:

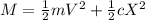`M=(1)/(2)mV^(2)+(1)/(2)cX^(2)` (2)

Now, according to the Conservation of the Energy Principle, and knowing there is not friction, the initial energy
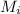`M_(i)` must be equal to the final energy
`M_(f)`:

`M_(i)=M_(f)` (3)

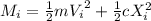`M_(i)=(1)/(2)m{V_(i)}^(2)+(1)/(2)c{X_(i)^(2)}` (4)

At the beginning, the block has a
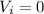`V_(i)=0`, because it starts from rest, this means the initial energy
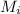`M_(i)` is only the Potential Elastic Energy:

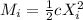`M_(i)=(1)/(2)c{X_(i)^(2)}` (5)

After the spring is compressed, is in its equilibrium point X=0, so
`X_(f)=0`. Then the block is released. This means the final energy
`M_(f)` is only the Kinetic Energy

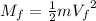`M_(f)=(1)/(2)m{V_(f)}^(2)` (6)

Now, we have to substitute (5) and (6) in (3):

`(1)/(2)c{X_(i)^(2)}=(1)/(2)m{V_(f)}^(2)`

`V_(f)=\sqrt{\frac{c{X_(i)^(2)}}{m}}`

`V_(f)= X_(i)\sqrt{(c)/(m)}`

`V_(f)=0.11m\sqrt{(368N/m)/(8.58kg)}`

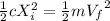
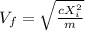
Finally:

`V_(f)=0.7203m/s`