Question

In trapezoid ABCD with legs AB and CD , diagonals BD ∩ AC =M so that BM:MD=1:4. Find AAMD, ACMD, and AACD if the area of AABM=8 in2.

Answer 1

Area of triangle AMD is 32 square inches.

Area of triangle CMD is 8 square inches.

Area of triangle ACD is 40 square inches.

Explanation:

In trapezoid ABCD with legs AB and CD.

Diagonal BD and AC intersect at M so that BM:MD=1:4

We are given ar(ABM)=8 in²

Ratio of area of two triangle is equal to ratio of their base.

`(ar(ABM))/(ar(AMD))=(BM)/(MD)`

`(8)/(ar(AMD))=(1)/(4)`

`ar(AMD)=32\text{ in}^2`

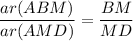
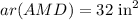
Thus, Area of triangle AMD is 32 square inches.

If two triangles lie on same base and same parallel line then their area is equal.

`\therefore ar(ABD)=ar(ACD)`

`ar(ACD)=ar(ACD)=ar(AMD)+ar(ABM)`

`ar(ACD)=8+32\Rightarrow 40\text{ in}^2`

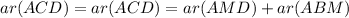
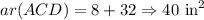
Thus, Area of triangle ACD is 40 square inches.

`ar(CMD)=ar(ACD)-ar(AMD)`

`ar(CMD)=40-32\Rightarrow 8\text{ in}^2`

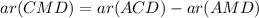
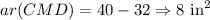
Thus, Area of triangle CMD is 8 square inches.