Answer:
52

Explanation:
We see that the radius of the big circle is 8m, and we see that the it is also the diameter of the second smallest circle. We also see that this diameter is split into two equal parts, and since the entire length is 8, each part will be 4. So what we need to do is find the area of each circle.
First we can start by finding the area of the smallest circle. The radius of this circle will be 4/2, 2. So the area of this circle will be

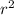 , and in this case 4
, and in this case 4
 .
.
Then we need to find the area of the bigger shaded portion, which will be the area of the big circle, minus the area of the smaller white circle.
First, lets find the are of the big circle, which again, will be

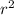 . This time, we plug in a radius of 8, and we get 64
. This time, we plug in a radius of 8, and we get 64
 .
.
Next we find the area of the smaller white circle, again

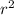 . We use a radius of 4 this time, giving us an area of 16
. We use a radius of 4 this time, giving us an area of 16
 .
.
Now we subtract the two values we found previously to find the area of the just the bigger shaded portion. That value will be 64
 -16
-16
 , which is 48
, which is 48

We then take 48
 , and we add the small shaded portion, which had an area of 4
, and we add the small shaded portion, which had an area of 4
 , and we add them, giving us a total of 52
, and we add them, giving us a total of 52
 .
.
Hope this helped.