Question

Write an equation for a line that is parallel to 2x+5y=15 and passes through the point (-10, 1)

Answer 1

Hey!

So the first thing we notice is that it says that the line is parallel to the line that we need to find. This means that the slope for both of the lines are the same. Now that we know we have to put the equation we are given into slope-intercept form to find the slope.

2x + 5y = 15

5y = -2x + 15

y = -(2/5)x + 3

Now we know that the slope for both the lines is -2/5. So we need to find the y-intercept or b. Since we also know a point on the line we can plug that into the slope-intercept form equation to with the slope to get b:

y = mx + b

1 = -(2/5)(-10) + b

1 = 4 + b

-3 = b

So the equation of the line would be:

y = -(2/5)x - 3

Answer 2

`y=-(2)/(5)x -3`

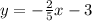
Explanation:

We are given the equation of a line
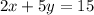`2x+5y=15` and we are supposed to find the equation of a line parallel to this which passes through a point
`(-10, 1)`.

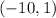Since the lines are parallel so they will have the same slope.

Changing the given equation to the standard form of equation
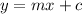`y=mx+c` to find the slope.

`2x+5y=15\\\\5y=-2x+15\\\\y=-(2)/(5)x + 3`

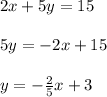
So the slope of the line is
`-(2)/(5)`

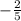
Finding the y-intercept:

`y=mx+c\\\\1=-(2)/(5) (-10)+c\\\\c=-3`

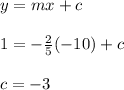
Therefore, the equation of line parallel to
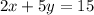`2x+5y=15` that passes through (-10, 1) is
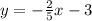`y=-(2)/(5) x-3`.