Answer:
(2, 7) or (-6, 1)
Explanation:
We are given two equations:
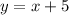 ; and
; and
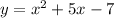
Since y is the subject for both the equations so we can put the values of y equal to each other to get:
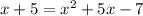
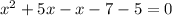
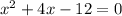
Factorizing the expression to get:
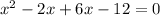
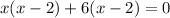
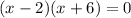
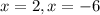
Putting x = 2 and x = -6 in any of the equations to get the values of y:
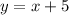
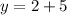
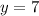
and
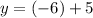
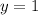
Therefore, solution to these equation is (2, 7) or (-6, 1).