Question

The area of the quadrilateral shown is 252 square inches. What is the perimeter?

(the width is 16.8 inches)

A. 61.8 inches
B. 31.8 inches
C. 63.6 inches
D. 67.2 inches

Answer 1

C. 63.6 inches

That is because to find the length of the quadrilateral do this since you already know the width of the polygon:

252/16.8 = 15

Now that we know the length do this since this is the formula to find the perimeter or for me I would just 2x:

2(16.8) + 2(15) =

33.6 + 30 = 63.6

The perimeter of the quadrilateral is 63.6 inches

Answer 2

The answer is 63.6
`in^2`

Explanation:

In order to determine the area of the quadrilateral, we have to know the values of its sides. The area of the quadrilateral is:

`A=a*b`

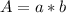
a= length of the quadrilateral

b=width of the quadrilateral

We know the area and the width of the quadrilateral, so we can determine its length:

`252=a*16.8\\a=(252)/(16.8)\\a=15`

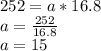
Then, the perimeter of the quadrilateral is:

P=2*a+2*b

P=2*15+2*16.8

P=63.6

Finally, the perimeter is 63.6
`in^2`