Question

Find f '(−3), if f(x) = (2x^2 − 7x)(−x^2 − 7). Round your answer to the nearest integer. Use the hyphen symbol, -, for negative values.

Answer 1

Answer:
`f'(-3)=538`

Step by step:

To get the derivative you can either multiply out the product (which I did below), or apply the formula for the derivative of a product of two functions. Either way you will obtain the same result, of course.

`f(x) = (2x^2-7x)(-x^2-7)=-2 x^4 + 7 x^3 - 14 x^2 + 49 x\\f'(x) = -8x^3 +21x^2 - 28x +49\\f'(-3)=538`

Answer 2

use product rule

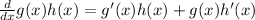`(d)/(dx) g(x)h(x)=g'(x)h(x)+g(x)h'(x)` (where the ' symbol is derivitive with respect to x, (just using Leibniz notation)

also remember the power rule:
`(d)/(dx) x^n=nx^(n-1)`

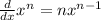
and sum rule,
`(d)/(dx) (g(x)+h(x))=(d)/(dx)g(x)+(d)/(dx)h(x)`

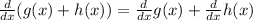
so first find the derivitive then evaluate it

if we say that
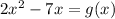`2x^2-7x=g(x)` and
`-x^2-7=h(x)`

setup:

find g'(x) and h'(x)

`g'(x)=2*2x^1-7*1x^0=4x-7*1=4x-7`

`h'(x)=2*(-x^1)-0=-2x`

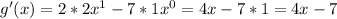
so
`f'(x)=g'(x)h(x)+g(x)h'(x)=(4x-7)(-x^2-7)+(2x^2-7x)(-2x)`

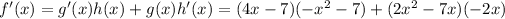
evaluate f'(-3)

`f'(-3)=(4(-3)-7)(-(-3)^2-7)+(2(-3)^2-7(-3))(-2(-3))`

`f'(-3)=(-19)(-16)+(39)(6)`

`f'(-3)=538`

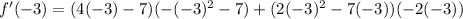
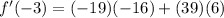
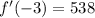
answer: f'(-3)=538