Answer:
B. (1.3, 2.3)
Explanation:
To find approximate solution of the system of equations, we need to equivate the two given equations and solve for x and y.
y = 4x - 3 and y = -5x + 9
4x - 3 = -5x + 9
Isolating the variables and constants, we get
4x + 5x = 9 + 3
9x = 12
Dividing both sides by 9, we get
x = 12 ÷ 9
x =
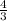
x = 1.3
Now plug in x =
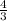 in the equation y = 4x - 3 to find the value of y.
in the equation y = 4x - 3 to find the value of y.
y = 4(
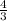 ) - 3
) - 3
y =
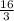 - 3
- 3
y =

y =
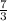
y = 2.3
So, x = 1.3 and y = 2.3 is the approximate solution.
Therefore, answer is B. (1.3, 2.3)