Question

V is inversely proportional to r^2 when r=2, v=12. The value of r is approximately 2.83 when v=

4

8

6

2

Answer 1

The correct answer option is 6.

Explanation:

We know that
`v` is inversely proportional to
`r^2` so we can write it as:

`v` ∝
`(1)/(r^2)`

To change the proportionality to equality, we need to have a constant k.

`v = (k)/(r^2)`

When
`r=2`then
`v=12` so we can find the value of the constant
`k`:

`12=(k)/(2^2)`

`k=48`

Now that we know the value of
`k`, we can find the value of
`v` when
`r=2.83`:

`v=(48)/(2.83^2)`

`v= 5.99` ≈
`6`

Answer 2

We are given

v is inversely proportional to r^2

so, we can write our equation as

`v=(k)/(r^2)`

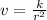
where

k is proportionality constant

we have

r=2 and v=12

so, we can use it and find k

`12=(k)/(2^2)`

`k=48`

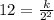
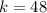
now, we can plug back k

`v=(48)/(r^2)`

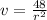
we can plug r=2.83

so, we can plug it and find v

`v=(48)/(2.83^2)`

`r=(48)/(8.0089)`

`v=5.9933`

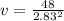
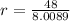
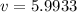
So, the approximate value of v is 6..........Answer