Question

Find the limit using L'Hospital's Rule
limx->0 (x-sinx)/x^3

Answer 1

Remember what L'Hospital's Rule tells us. It says the following.

If
`\lim _(x \rightarrow a)\frac {f\left( x\right) }{g\left( x\right) } = (0)/(0) \,\,\textrm{or} \,\,\lim_(x \to a) (f(x))/(g(x)) = (\pm \infty)/(\pm \infty)`

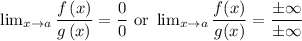
Then
`\lim_(x \to a)(f(x))/(g(x)) = \lim_(x \to a) (f'(x))/(g'(x))`

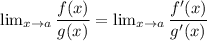
We know that
`\lim _(x\rightarrow 0)\left( x-\sin x\right) =0` using direct substitution and
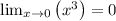`\lim _(x\rightarrow 0)\left( x^(3)\right) =0` through direct substitution as well. Thus, we can find the derivatives of the numerator and denominator and find our limit.

`(d)/(dx)[x - \sin x] = 1 - \cos x`

`\frac {d}{dx}\left[ x^(3)\right] =3x^(2)`

Thus, we are now trying to find:

`\lim _(x\rightarrow 0)\frac {1-\cos x}{3x^(2)}`

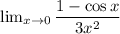
To do this, we can use direct substitution for both the numerator and denominator.

`\lim _(x\rightarrow 0)(1-\cos x)=1-1=0`

`\lim _(x\rightarrow 0)\left( 3x^(2)\right) =0`

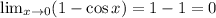
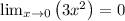
Again, we have the following:

`\lim_(x \to 0) (1 - \cos x)/(3x^2) = (0)/(0)`

Thus, we are going to have to use L'Hospital's Rule again.

`\frac {d}{dx}\left[ 1-\cos x\right] =\sin x`

`\frac {d}{dx}\left[ 3x^(2)\right] =6x`

Now, we are trying to find the following:

`\lim _(x\rightarrow 0)\left( \frac {\sin x}{6x}\right)`

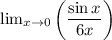
Let's find the limits of the numerator and denominator and set them over each other to find the answer to this limit.

`\lim _(x\rightarrow 0)\left( \sin x\right) =0`

`\lim _(x\rightarrow 0)\left( 6x\right) =0`

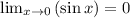
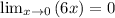
Again, we are going to have to L'Hospital's Rule to find the limit since the answer to our limit is:

`\lim _(x\rightarrow 0)\left( \frac {\sin x}{6x}\right) =\frac {0}{0}`

`\frac {d}{dx}\left[ \sin x\right] =\cos x`

`\frac {d}{dx}\left( 6x\right) =6`

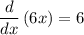
Now, we are trying to find:

`\lim _(x\rightarrow 0)\left( \frac {\cos x}{6}\right)`

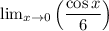
We are going to use direct substitution to find the limits of the numerator and denominator to find the answer.

`\lim _(x\rightarrow 0)\left( \cos x\right) =1`

`\lim _(x\rightarrow 0)\left( 6\right) =6`

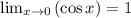
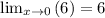
Thus, the answer to this limit is:

`\lim _(x\rightarrow 0)\left( \frac {\cos x}{6}\right) =\frac {1}{6}`

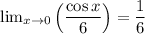
Our answer is 1/6.