Question

Find the sum of the first 63 terms of –19, -13, -7 …

Answer 1

The Given Sequence is an Arithmetic Sequence with First term = -19

⇒ a = -19

Second term is -13

We know that Common difference is Difference of second term and first term.

⇒ Common Difference (d) = -13 + 19 = 6

We know that Sum of n terms is given by :
`S_n = (n)/(2)(2a + (n - 1)d)`

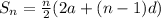
Given n = 63 and we found a = -19 and d = 6

`\implies S_6_3 = (63)/(2)(2(-19) + (63 - 1)6)`

`\implies S_6_3 = (63)/(2)(-38 + (62)6)`

`\implies S_6_3 = (63)/(2)(-38 + 372)`

`\implies S_6_3 = (63)/(2)(-38 + 372)`

`\implies S_6_3 = (63)/(2)(334)`

`\implies S_6_3 = {63}(167) = 10521`

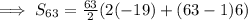
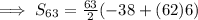
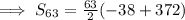
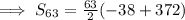
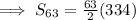
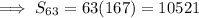
The Sum of First 63 terms is 10521