Question

For the function f(x) = 4x^3 -36x^2 + 5: (a) find the critical numbers, (b) find the open intervals where the function is increasing or decreasing; and (c) apply the first derivative test to identify all relative extrema.

Answer 1

`\bf f(x)=4x^3-36x^2+5\implies \cfrac{df}{dx}=12x^2-72x\implies \stackrel{\textit{setting the derivative to 0}}{0=12x(x-6)} \\\\\\ x= \begin{cases} 0\\ 6 \end{cases}`

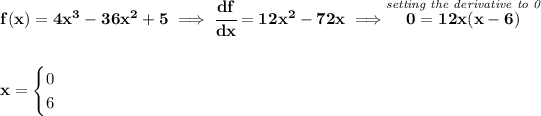
so we have those critical values, which gives us the intervals of (-∞, 0] , [0, 6] and [6, +∞).

where is it increasing or decreasing? well, that's just a matter of checking a value on each region for the the first derivative, namely the first derivative test.

we can check for f(-1) = 12(-1)² - 72(-1), is a positive value, increasing.

and check f(1) = 12(1)² - 72(1), is a negative value, decreasing.

and check f(7) = 12(7)² - 72(7), positive, so increasing.

check the picture below, and you can see there which are the minima or maxima.