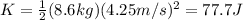Question

He law of conservation of energy states that energy is constant in a closed system.

• Using a bouncing ball as an example, describe the conservation of energy.
• Give at least three examples of the conservation of energy in everyday life.

Using a bouncing ball as an example, describe the conservation of energy. Give at least three examples of the conservation of energy in everyday life. Press Space or enter key to Enter Text (9000) The gravitational potential energy of the wrecking ball on a demolition machine is measured by its mass and height. A particular ball has a mass of 200.0 kg. What is the gravitational potential energy of the ball relative to the ground when the crane has raised the ball 35 meters? (The acceleration due to gravity on Earth is 9.8 m/s2

.) The gravitational potential energy of the wrecking ball on a demolition machine is measured by its mass and height. A particular ball has a mass of 200.0 kg. What is the gravitational potential energy of the ball relative to the ground when the crane has raised the ball 35 meters? (The acceleration due to gravity on Earth is 9.8 m/s 2 9.8 m/s2 .) Press Space or enter key to Enter Text (9000) Potential energy is the energy stored in an object, and kinetic energy is the energy of motion.a. Suppose it takes a force of 12 newtons to stretch a spring to 25.0 cm. Calculate the elastic potential energy of the spring stretched to 25.0 cm. Potential energy is the energy stored in an object, and kinetic energy is the energy of motion. a. Suppose it takes a force of 12 newtons to stretch a spring to 25.0 cm. Calculate the elastic potential energy of the spring stretched to 25.0 cm. Press Space or enter key to Enter Text (9000) b. Calculate the magnitude of the kinetic energy of a mass of 8.6 kg moving with a speed of 4.25 m/s. b. Calculate the magnitude of the kinetic energy of a mass of 8.6 kg moving with a speed of 4.25 m/s. Press Space or enter key to Enter Text (9000)

Answer 1

1a) The bouncing ball is an example of continuous conversion between kinetic energy and gravitational potential energy. In fact, as the ball goes upward, it slows down (so, its kinetic energy decreases) and its height increases (so, its potential energy increases). On the contrary, when the ball goes downward, it speeds up (so, its kinetic energy increases) and its height decreases (so, its potential energy decreases). The total mechanical energy, which is sum of the kinetic and potential energy:

`E=K+U`

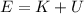
remains constant (if we neglect air resistance and friction), so the energy is continuously converted between the two forms of energy.

1b)

Example 1: a ball left falling from a building - initially, the ball has gravitational potential energy, which is then converted into kinetic energy as the ball falls down and its speed increases.

Example 2: a child sliding on a ramp - also in this case, the child has initially gravitational potential energy, which is then converted into kinetic energy as the child slides down and his speed increases.

Example 3: an arrow fired vertically upward - initially, the arrow has only kinetic energy (due to its speed). As the arrow goes higher, its speed decreases (so, kinetic energy decreases), while the height increases, and so the energy is converted into gravitational potential energy.

2) 68600 J

The formula for the gravitational potential energy of the wrecking ball is:

`U=mgh`

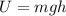
where

m = 200.0 kg is the mass of the ball

g = 9.8 m/s^2 is the acceleration due to gravity

h = 35 m is the height of the ball relative to the ground

Substituting into the formula, we find

`U=mgh=(200.0 kg)(9.8 m/s^2)(35 m)=68600 J`

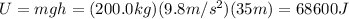
3a) 1.5 J

First of all, we can calculate the spring constant of the spring, which is given by the ratio between the force applied (12 N) and the stretching (25 cm=0.25 m):

`k=(F)/(x)=(12 N)/(0.25 m)=48 N/m`

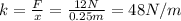
And now we can calculate the elastic potential energy stored in the spring, with the formula:

`U=(1)/(2)kx^2=(1)/(2)(48 N/m)(0.25 m)^2=1.5 J`

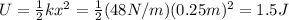
3b) 77.7 J

The kinetic energy of an object is given by:

`K=(1)/(2)mv^2`

where

m is the mass of the object

v is its speed

In this problem, m=8.6 kg and v=4.25 m/s, so the kinetic energy is

`K=(1)/(2)(8.6 kg)(4.25 m/s)^2=77.7 J`