Question

A circle is centered at the point (5, -4) and passes through the point (-3, 2).

The equation of this circle is (x + _ )2 + (y + _ )2 = _
.

Answer 1

`(x-5)^2+(y+4)^2 = 10^2`

Explanation:

The formula for the equation of a circle centered at the origin (0, 0) is
`x^2+y^2 = r^2` but when the center of the circle is not the origin, then you move it back to the center mathematically.

So we have:

`(x-5)^2+(y+4)^2 = r^2`

Finding the radius
`r` by calculating the distance from the center to the given point:

`r= √((5-(-3))^2+(-4-2)^2) = √(64+36) = √(100) = 10`

Therefore, the equation of this circle will be:

`(x-5)^2+(y+4)^2 = 10^2`

Answer 2

By definition, the equation of a circle, centered at point (a, b) is

`(x-a) ^ 2 + (y-b) ^ 2 = r ^ 2`

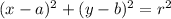
Where r is the radius of the circumference, and is calculated as the distance from the center to any point belonging to the circumference.

We have the center (5, -4) and the point through which the circumference passes (-3, 2), then:

`a = 5\\b = -4\\r = \sqrt {(- 3-5) ^ 2 + (2 + 4) ^ 2}\\r = 10`

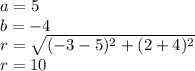
Finally, the equation of the circumference is:

`(x-5) ^ 2 + (y + 4) ^ 2 = 10 ^ 2`