I cannot just answer part (c) because it is dependent on previous answers. So, let's go through parts (a) and (b) so we can then answer (c).
For part a, understand that critical points are points in a function f(x) where the derivative of the function f'(x) is either equal to 0 or it does not exist. Let's take the derivative of this function, using quotient rule which states that:
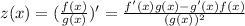
In our case, f(x) = x + 7 and g(x) = x + 1. Following the rule, our derivative will be:

Let's simplify that:
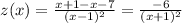
Notice that the above function is never equal to 0 (numerator never equals 0, so the function follows). It is, however, undefined at x = -1 as the denominator is 0:
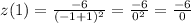
This gives us a divide by 0 error, therefore it is undefined. This is a critical point, so your answer to part (a) should be changed to "The critical number(s) is/are -1.
For part (b) it asks if the function is ever increasing. For a function to be increasing over some interval, the derivative of that function must be positive. Notice that even if we plug in a negative number for the denominator, the derivative will never be positive because the denominator is squared, meaning we will always have a positive denominator. Our numerator will always be negative no matter what, so a negative number over a positive number will always equal a negative number suggesting that our function will never be increasing. Let's try a negative number: x = -2:
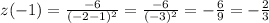
Therefore, your answer to part (b) is correct! Good job!
For part (c) we must identify any interval for which the function is decreasing. We just figured out that our function is always decreasing. Even if we plug in a negative number. But, we have a little "plot-twist." The function is undefined at x = -1, therefore, it is not decreasing at that single point. We write that as:
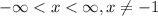
or, we can also write it as:
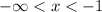 and
and

We write it in interval notation as: (-∞, -1) and (-1, ∞).
So, your answer to part (c) must be one of the above. We have answered all of the questions. Hope I could help! :)